单词查找数 - Axlis ~ Blog

单词查找数 February 10, 2022

单词查找树

单词查找树是一种已知字符集的字符串查找树, 读作"try".

初始状态

假定字符集为{x, y, z}, 节点相应位置为0表示绝对没有以其结尾的字符串.

1-1

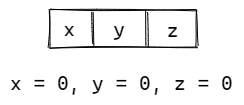
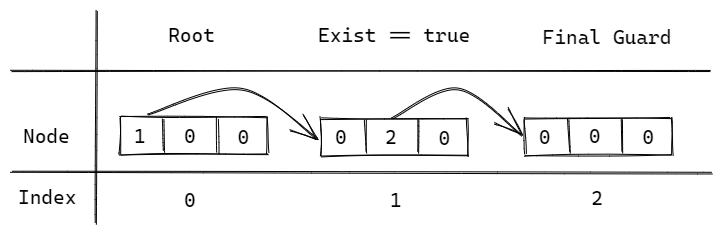
填充状态

现在的状态是插入字符串xy后的状态, 叶子节点一定是一个全空节点, 作为最后的守卫.

该表示法通过索引值表示链接关系, 展开后就是一个度为字符集大小的查找树.

1-2

具体实现

class Trie {
private:
    vector<array<int, 26>> nodes;
    vector<bool>           exist;
    vector<int>            tags; // 维护存在性之外的状态.

    int size = 0;

public:
    Trie() : nodes(1), exist(1), tags(1) {}

    void insert(const string &str) {
        int current = 0;

        for (char c : str) {
            c -= 'a';

            if (c < 0 || c >= 26) {
                throw runtime_error("@1: invalid character");
            }

            if (current == nodes.size()) {
                nodes.emplace_back();
            }

            if (nodes[current][c] == 0) {
                nodes[current][c] = ++size; // 链接到下一个节点.
            }

            current = nodes[current][c];
        }

        // 补齐叶子节点.
        nodes.resize(current + 1);
        exist.resize(current + 1);
        tags.resize(current + 1);

        exist[current] = true;
    }

    int find(const string &str) {
        int current = 0;

        for (char c : str) {
            c -= 'a';

            if (c < 0 || c >= 26) {
                throw runtime_error("@2: invalid character");
            }

            if (nodes[current][c] == 0) {
                return 0; // 找到了叶子节点.
            }

            current = nodes[current][c];
        }

        return getTag(current);
    }

private:
    static const int UNUSED = 0;
    static const int USED   = 1;

    int getTag(int pos) {
        if (!exist[pos]) {
            return 0;
        }

        if (tags[pos] == UNUSED) {
            tags[pos] = USED;
            return 1;
        }

        return 2;
    }
};

这里只针对ACM使用场景简单实现了少了API, 另外将节点单独封装成一个单独的类会是一个不错的改进!

扩展资料

Algorithm 4th Edition By Robert Sedgewick

Trie